El cuadrado mágico es una invención oriental, concretamente de la India y de China. Dicho cuadrado no es más que una tabla con el mismo número de casillas verticales (columnas) que horizontales (líneas), y son calificados mágicos por las extrañas características y propiedades que poseen.

En la antigua China ya se conocían los cuadrados mágicos desde el III milenio a. C. Según la leyenda, un cierto día se produjo el desbordamiento de un río; la gente, temerosa, intentó hacer una ofrenda al dios del río Lo (uno de los desbordados) para calmar su ira. Sin embargo, cada vez que lo hacían, aparecía una tortuga que rondaba la ofrenda sin aceptarla, hasta que un chico se dio cuenta de las peculiares marcas del caparazón de la tortuga, de este modo pudieron incluir en su ofrenda la cantidad pedida (15), quedando el dios satisfecho y volviendo las aguas a su cauce.

Igualmente conocieron combinaciones de esta clase los indios, egipcios, árabes y griegos. A tales cuadrados, las diferentes culturas les han atribuido propiedades astrológicas y adivinatorias portentosas, grabándose con frecuencia en talismanes.

Naturalmente, no todos los cuadrados mágicos son igual de difíciles. Su dificultad reside en el número de casillas. Así, cuantas más casillas tiene la figura, más complicada es.

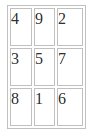
He aquí un cuadrado mágico chino muy sencillo, con una antigüedad de 6000 años. Ya está resuelto. Como veis, el resultado de la suma de las líneas es el mismo que el de las diagonales y el de las columnas:

Ahora os propongo otro cuadrado mágico. Vuestra misión será completarlo de tal manera que la suma del cuadrado central sea la misma que la suma de las columnas, las líneas y las diagonales. Los números que se deben colocar van del 1 al 16. Además, la suma de columnas, líneas y cuadrado central es 34.  ¡Buena suerte!

Comentario: ¡Muy bien, Alejandro y Jaled!. La respuesta correcta a La contraseña era contar las letras de la palabra que indica cada número. A ver que tal se os dan los cuadrados mágicos.